Composite decking material captures carbon dioxide
Could our choice of patio decking help reduce the global warming effects of building materials?
Fuel curiosity in science careers
Help foster the next generation of scientists by linking teaching topics to real-world events and career pathways
Use AI to successfully assess students’ understanding
Discover how to quickly and effectively generate multiple choice questions on key chemistry topics
5 ways to successfully teach structure and bonding at 14–16
Strengthen students’ grasp of the abstract so they master this tricky topic and effectively tackle exam questions
Illustrate polymer properties with a self-siphoning solution
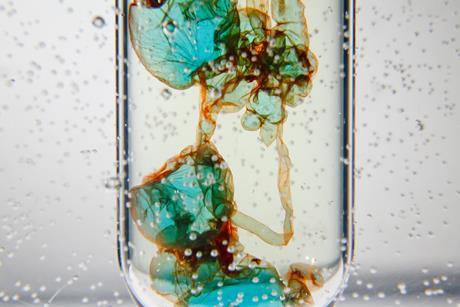
Demonstrate concentration and density with a transition metal colloid cell
Highlight transition metal chemistry with an oscillating luminol reaction
Reversible reactions with transition metal complexes
Demonstrate changes of state using volume differences
- Previous
- Next
How visuospatial thinking boosts chemistry understanding
Encourage your students to use their hands to help them get to grips with complex chemistry concepts
Understanding how students untangle intermolecular forces
Discover how learners use electronegativity to predict the location of dipole−dipole interactions
3 ways to boost knowledge transfer and retention
Apply these evidence-informed cognitive processes to ensure your learners get ahead
Why we should ditch working scientifically
Explore a new approach to this this national curriculum strand, grounded in contemporary cognitive science
How do you feel about working in science education?
Tell us what it’s like by taking part in the Science teaching survey, and we can improve our support for you
Why I use video to teach chemistry concepts
Helen Rogerson shares why and when videos are useful in the chemistry classroom